1. 算法思路

DBSCAN算法的核心是“延伸”。先找到一个未访问的点p，若该点是核心点，则创建一个新的簇C，将其邻域中的点放入该簇，并遍历其邻域中的点，若其邻域中有点q为核心点，则将q的邻域内的点也划入簇C，直到C不再扩展。直到最后所有的点都标记为已访问。

点p通过密度可达来扩大自己的“地盘”，实际上就是簇在“延伸”。

图示网站：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/ 可以看一下簇是如何延伸的。

2. 算法实现

2.1 计算两点之间的距离

# 计算两个点之间的欧式距离，参数为两个元组
def dist(t1, t2):
    dis = math.sqrt((np.power((t1[0]-t2[0]),2) + np.power((t1[1]-t2[1]),2)))
    # print("两点之间的距离为："+str(dis))
    return dis

2.2 读取文件，加载数据集

def loadDataSet(fileName, splitChar='\t'):
    dataSet = []
    with open(fileName) as fr:
        for line in fr.readlines():
            curline = line.strip().split(splitChar)
            fltline = list(map(float, curline))
            dataSet.append(fltline)
    return dataSet

2.3 DBSCAN算法实现

1、标记点是否被访问：我设置了两个列表，一个存放未访问的点unvisited，一个存放已访问的点visited。每次访问一个点，unvisited列表remove该点，visited列表append该点，以此来实现点的标记改变。

2、C作为输出结果，初始时是一个长度为所有点的个数的值全为-1的列表。之后修改点对应的索引的值来设置点属于哪个簇

# DBSCAN算法，参数为数据集，Eps为指定半径参数，MinPts为制定邻域密度阈值
def dbscan(Data, Eps, MinPts):
    num = len(Data)  # 点的个数
    # print("点的个数："+str(num))
    unvisited = [i for i in range(num)]  # 没有访问到的点的列表
    # print(unvisited)
    visited = []  # 已经访问的点的列表
    C = [-1 for i in range(num)]
    # C为输出结果，默认是一个长度为num的值全为-1的列表
    # 用k来标记不同的簇，k = -1表示噪声点
    k = -1
    # 如果还有没访问的点
    while len(unvisited) > 0:
        # 随机选择一个unvisited对象
        p = random.choice(unvisited)
        unvisited.remove(p)
        visited.append(p)
        # N为p的epsilon邻域中的对象的集合
        N = []
        for i in range(num):
            if (dist(Data[i], Data[p]) <= Eps):# and (i!=p):
                N.append(i)
        # 如果p的epsilon邻域中的对象数大于指定阈值，说明p是一个核心对象
        if len(N) >= MinPts:
            k = k+1
            # print(k)
            C[p] = k
            # 对于p的epsilon邻域中的每个对象pi
            for pi in N:
                if pi in unvisited:
                    unvisited.remove(pi)
                    visited.append(pi)
                    # 找到pi的邻域中的核心对象，将这些对象放入N中
                    # M是位于pi的邻域中的点的列表
                    M = []
                    for j in range(num):
                        if (dist(Data[j], Data[pi])<=Eps): #and (j!=pi):
                            M.append(j)
                    if len(M)>=MinPts:
                        for t in M:
                            if t not in N:
                                N.append(t)
                # 若pi不属于任何簇，C[pi] == -1说明C中第pi个值没有改动
                if C[pi] == -1:
                    C[pi] = k
        # 如果p的epsilon邻域中的对象数小于指定阈值，说明p是一个噪声点
        else:
            C[p] = -1

    return C

3. 问题记录

代码思路非常简单，让我以为实现起来也很简单。结果拖拖拉拉半个多月才终于将算法改好。

算法实现过程中遇到的问题其实是小问题，但是导致的结果非常严重。因为不起眼所以才难以察觉。

这是刚开始我运行算法得到的结果（Eps为10，MinPts为10）：

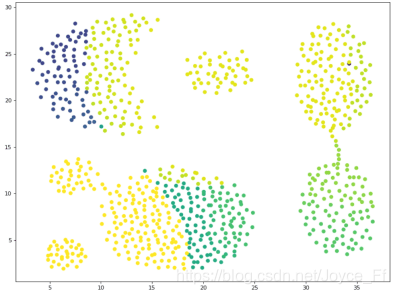
Eps为2，MinPts为10（我改了点的大小）：

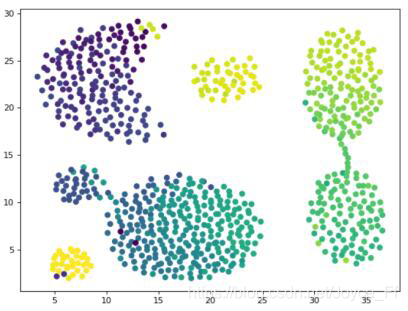
可以看出图中颜色特别多，实际上就是聚成的簇太多，可实际上目测应该只有七八个簇。这是为什么呢？

原来是变量k的重复使用问题。

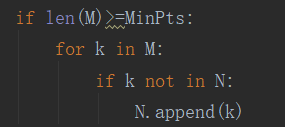
前面我用k来标识不同的簇，后面（如下图）我又将k变成了循环变量，注意M列表中都是整数，代表点在数据集中的索引，所以实际上是k在整数列表中遍历，覆盖掉了前面用来标识不同簇的k值，导致每次运行出来k取值特别多（如下下图）。

4. 运行结果

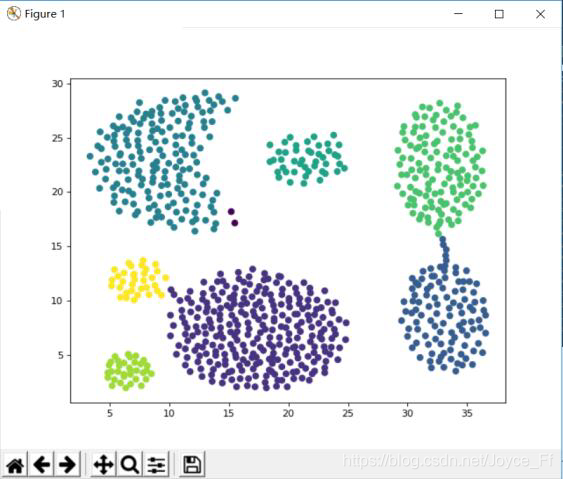
5. 完整代码

5.1 源数据

附数据集

链接：数据集788个点
提取码：rv06

5.2 源代码

# encoding:utf-8
import matplotlib.pyplot as plt
import random
import numpy as np
import math
from sklearn import datasets

list_1 = []
list_2 = []
# 数据集一：随机生成散点图,参数为点的个数
# def scatter(num):
#     for i in range(num):
#         x = random.randint(0, 100)
#         list_1.append(x)
#         y = random.randint(0, 100)
#         list_2.append(y)
#     print(list_1)
#     print(list_2)
#     data = list(zip(list_1, list_2))
#     print(data)
#     #plt.scatter(list_1, list_2)
#     #plt.show()
#     return data
#scatter(50)

def loadDataSet(fileName, splitChar='\t'):
    dataSet = []
    with open(fileName) as fr:
        for line in fr.readlines():
            curline = line.strip().split(splitChar)
            fltline = list(map(float, curline))
            dataSet.append(fltline)
    return dataSet

# 计算两个点之间的欧式距离，参数为两个元组
def dist(t1, t2):
    dis = math.sqrt((np.power((t1[0]-t2[0]),2) + np.power((t1[1]-t2[1]),2)))
    # print("两点之间的距离为："+str(dis))
    return dis

# dis = dist((1,1),(3,4))
# print(dis)


# DBSCAN算法，参数为数据集，Eps为指定半径参数，MinPts为制定邻域密度阈值
def dbscan(Data, Eps, MinPts):
    num = len(Data)  # 点的个数
    # print("点的个数："+str(num))
    unvisited = [i for i in range(num)]  # 没有访问到的点的列表
    # print(unvisited)
    visited = []  # 已经访问的点的列表
    C = [-1 for i in range(num)]
    # C为输出结果，默认是一个长度为num的值全为-1的列表
    # 用k来标记不同的簇，k = -1表示噪声点
    k = -1
    # 如果还有没访问的点
    while len(unvisited) > 0:
        # 随机选择一个unvisited对象
        p = random.choice(unvisited)
        unvisited.remove(p)
        visited.append(p)
        # N为p的epsilon邻域中的对象的集合
        N = []
        for i in range(num):
            if (dist(Data[i], Data[p]) <= Eps):# and (i!=p):
                N.append(i)
        # 如果p的epsilon邻域中的对象数大于指定阈值，说明p是一个核心对象
        if len(N) >= MinPts:
            k = k+1
            # print(k)
            C[p] = k
            # 对于p的epsilon邻域中的每个对象pi
            for pi in N:
                if pi in unvisited:
                    unvisited.remove(pi)
                    visited.append(pi)
                    # 找到pi的邻域中的核心对象，将这些对象放入N中
                    # M是位于pi的邻域中的点的列表
                    M = []
                    for j in range(num):
                        if (dist(Data[j], Data[pi])<=Eps): #and (j!=pi):
                            M.append(j)
                    if len(M)>=MinPts:
                        for t in M:
                            if t not in N:
                                N.append(t)
                # 若pi不属于任何簇，C[pi] == -1说明C中第pi个值没有改动
                if C[pi] == -1:
                    C[pi] = k
        # 如果p的epsilon邻域中的对象数小于指定阈值，说明p是一个噪声点
        else:
            C[p] = -1

    return C


# 数据集二：788个点
dataSet = loadDataSet('788points.txt', splitChar=',')
C = dbscan(dataSet, 2, 14)
print(C)
x = []
y = []
for data in dataSet:
    x.append(data[0])
    y.append(data[1])
plt.figure(figsize=(8, 6), dpi=80)
plt.scatter(x,y, c=C, marker='o')
plt.show()
# print(x)
# print(y)