机器学习系列之决策树算法（02）：决策树的生成

1. 前言

上文讲到决策树的特征选择会根据不同的算法选择不同的分裂参考指标，例如信息增益、信息增益比和基尼指数，本文完整分析记录决策树的详细生成过程和剪枝处理。

2. 决策树的生成

示例数据表格

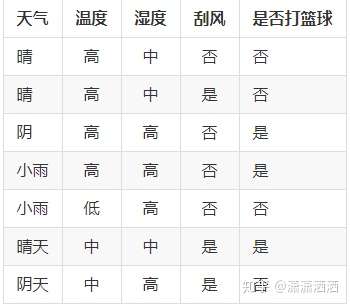
    文章所使用的数据集如下，来源于《数据分析实战45讲》17讲中

2.1 相关概念阐述

2.1.1 决策树

 以上面的表格数据为例，比如我们考虑要不要去打篮球，先看天气是不是阴天，是阴天的话，外面刮风没，没刮风我们就去，刮风就不去。决策树就是把上面我们判断背后的逻辑整理成一个结构图，也就是一个树状结构。

2.1.2 ID3、C4.5、CART

在决策树构造中有三个著名算法：ID3、C4.5、CART，ID3算法计算的是信息增益，C4.5计算使用的是增益率、CART计算使用的是基尼系数，关于这部分内容可以参考上文【机器学习系列之决策树算法（01）：决策树特征选择】下面简单介绍下其算法，这里也不要求完全看懂，扫一眼有个印象就行，在后面的例子中有计算示例，回过头结合看应该就懂了。

信息熵

 在信息论中，随机离散事件的出现的概率存在不确定性，为了衡量这种信息的不确定性，信息学之父香农引入了信息熵的概念，并给出了计算信息熵的数学公式。

​ Entopy(t)=-Σp(i|t)log2p(i|t)

信息增益

信息增益指的是划分可以带来纯度的提高，信息熵的下降。特征的信息熵越大代表特征的不确定性越大，代表得知了该特征后，数据集的信息熵会下降更多，即信息增益越大。它的计算公式是父亲节点的信息熵减去所有子节点的信息熵。信息增益的公式可以表示为：

​ Gain(D,a)=Entropy(D)- Σ|Di|/|D|Entropy(Di)

信息增益率

 信息增益率 = 信息增益 / 属性熵。属性熵，就是每种属性的信息熵，比如天气的属性熵的计算如下,天气有晴阴雨,各占3/7,2/7,2/7：

​ H(天气)= -(3/7 * log2(3/7) + 2/7 * log2(2/7) + 2/7 * log2(2/7))

基尼系数

 基尼系数在经济学中用来衡量一个国家收入差距的常用指标.当基尼指数大于0.4的时候,说明财富差异悬殊.基尼系数在0.2-0.4之间说明分配合理,财富差距不大.扩展阅读下基尼系数

 基尼系数本身反应了样本的不确定度.当基尼系数越小的时候,说明样本之间的差异性小,不确定程度低.

 CART算法在构造分类树的时候,会选择基尼系数最小的属性作为属性的划分.

 基尼系数的计算公式如下:

​ Gini = 1 – Σ (Pi)2 for i=1 to number of classes

2.2 完整生成过程

 下面是一个完整的决策树的构造生成过程，已完整开头所给的数据为例

2.2.1 根节点的选择

 在上面的列表中有四个属性:天气,温度,湿度,刮风.需要先计算出这四个属性的信息增益、信息增益率、基尼系数

 数据集中有7条数据，3个打篮球，4个不打篮球，不打篮球的概率为4/7,打篮球的概率为3/7,则根据信息熵的计算公式可以得到根节点的信息熵为：

​ Ent(D)=-(4/7 * log2(4/7) + 3/7 * log2(3/7))=0.985

天气

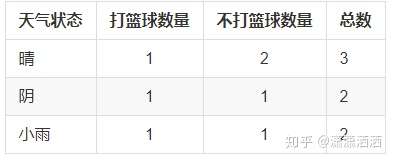
    其数据表格如下:

信息增益计算

如果将天气作为属性划分，分别会有三个叶节点：晴天、阴天、小雨，其中晴天2个不打篮球，1个打篮球；阴天1个打篮球，1个不打篮球；小雨1个打篮球，1个不打篮球，其对应相应的信息熵如下：

D(晴天)=-(1/3 * log2(1/3) + 2/3 * log2(2/3)) = 0.981

D(阴天)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

D(雨天)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

在数据集中晴天有3条数据，阴天有2条数据，雨天有2条数据，对应的概率为3/7、2/7、2/7，那么作为子节点的归一化信息熵为：

3/7 * 0.918 + 2/7 * 1.0 * 2/7 * 1.0 = 0.965

其信息增益为：

Gain(天气)=0.985 - 0.965 = 0.020

信息增益率计算

 天气有三个选择，晴天有3条数据，阴天有2条数据，雨天有2条数据，对应的概率为3/7、2/7、2/7，其对应的属性熵为：

H(天气)=-(3/7 * log2(3/7) + 2/7 * log2(2/7) + 2/7 * log2(2/7)) = 1.556

 则其信息增益率为：

Gain_ratio(天气)=0.020/1.556=0.012

基尼系数计算

• Gini(天气=晴)=1 - (1/3)^2 - (2/3)^2 = 1 - 1/9 - 4/9 = 4/9
• Gini(天气=阴)=1 - (1/2)^2 - (1/2)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(天气=小雨)=1 - (1/2)^2 - (1/2)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(天气)=(3/7) * 4/9 + (2/7) * 0.5 + (2/7) * 0.5 = 4/21 + 1/7 + 1/7 = 10/21

温度

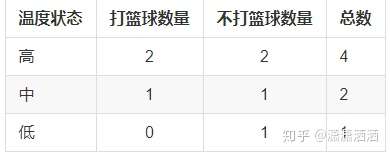
  其数据表格如下:

信息增益计算

    各情况的信息熵如下：

D(高)=-(2/4 * log2(2/4) + 2/4 * log2(2/4)) = 1.0

D(中)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

D(低)=-(0/1 * log2(0/1) + 1/1 * log2(1/1)) = 0.0

    作为子节点的归一化信息熵为：

4/7 * 1.0 + 2/7 * 1.0 * 1/7 * 0.0 = 0.857

    其信息增益为：

Gain(温度)=0.985 - 0.857 = 0.128

信息增益率计算

    属性熵为：

H(温度)=-(4/7 * log2(4/7) + 2/7 * log2(2/7) + 1/7 * log2(1/7)) = 1.378

    则其信息增益率为：

Gain_ratio(温度)=0.128/1.378=0.0928

基尼系数计算

• Gini(温度=高)=1 - (2/4)^2 - (2/4)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(温度=中)=1 - (1/2)^2 - (1/2)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(温度=低)=1 - (0/1)^2 - (1/1)^2 = 1 - 0 - 1 = 0
• Gini(温度)=4/7 * 0.5 + 2/7 * 0.5 + 1/7 * 0 = 3/7

湿度

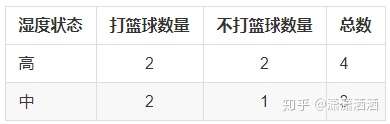
    其数据表格如下:

信息增益计算

    各情况的信息熵如下：

D(高)=-(2/4 * log2(2/4) + 2/4 * log2(2/4)) = 1.0

D(中)=-(2/3 * log2(2/3) + 1/3 * log2(1/3)) = 0.918

    作为子节点的归一化信息熵为：

4/7 * 1.0 + 3/7 * 0.918 = 0.964

    其信息增益为：

Gain(湿度)=0.985 - 0.964 = 0.021

信息增益率计算

    属性熵为：

H(湿度)=-(4/7 * log2(4/7) + 3/7 * log2(3/7) = 0.985

    则其信息增益率为：

Gain_ratio(湿度)=0.021/0.985=0.021

基尼系数计算

• Gini(湿度=高)=1 - (2/4)^2 - (2/4)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(湿度=中)=1 - (2/3)^2 - (1/3)^2 = 1 - 4/9 - 1/9 = 4/9
• Gini(湿度)=(4/7) * 0.5 + (3/7) * 4/9 = 2/7 + 4/21 = 10/21 ~ 0.47619

刮风

    其数据表格如下:

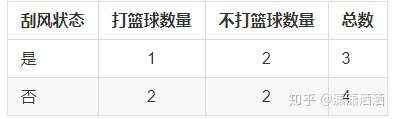
信息增益计算

    各情况的信息熵如下：

D(是)=-(2/3 * log2(2/3) + 1/3 * log2(1/3)) = 0.918

D(否)=-(2/4 * log2(2/4) + 2/4 * log2(2/4)) = 1.0

    作为子节点的归一化信息熵为：

3/7 * 1.0 + 4/7 * 0.918 = 0.964

    其信息增益为：

Gain(刮风)=0.985 - 0.964 = 0.021

信息增益率计算

    属性熵为：

H(刮风)=-(4/7 * log2(4/7) + 3/7 * log2(3/7) = 0.985

    则其信息增益率为：

Gain_ratio(刮风)=0.021/0.985=0.021

基尼系数计算

• Gini(刮风=是)=1 - (2/3)^2 - (1/3)^2 = 1 - 4/9 - 1/9 = 4/9
• Gini(刮风=否)=1 - (2/4)^2 - (2/4)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(刮风)=(4/7) * 0.5 + (3/7) * 4/9 = 2/7 + 4/21 = 10/21 ~ 0.47619

根节点的选择

  如下汇总所有接口,第一个为信息增益的，第二个为信息增益率的，第三个为基尼系数的。其中信息增益和信息增益率选择最大的，基尼系数选择最小的。从下面的结果可以得到选择为：温度

信息增益

• Gain(天气)=0.985 - 0.965 = 0.020

• Gain(温度)=0.985 - 0.857 = 0.128

• Gain(湿度)=0.985 - 0.964 = 0.021

• Gain(刮风)=0.985 - 0.964 = 0.021

信息增益率

• Gain_ratio(天气)=0.020/1.556=0.012
• Gain_ratio(温度)=0.128/1.378=0.0928
• Gain_ratio(湿度)=0.021/0.985=0.021
• Gain_ratio(刮风)=0.021/0.985=0.021

基尼系数

• Gini(天气)=(3/7) * 4/9 + (2/7) * 0.5 + (2/7) * 0.5 = 0.47619
• Gini(温度)=4/7 * 0.5 + 2/7 * 0.5 + 1/7 * 0 = 0.42857
• Gini(湿度)=(4/7) * 0.5 + (3/7) * 4/9 = 2/7 + 4/21 = 10/21 ~ 0.47619
• Gini(刮风)=(4/7) * 0.5 + (3/7) * 4/9 = 2/7 + 4/21 = 10/21 ~ 0.47619

确定根节点以后,大致的树结构如下，温度低能确定结果，高和中需要进一步的进行分裂，从剩下的数据中再次进行属性选择:

• 根节点
  • 子节点温度高:(待进一步进行选择)
  • 子节点温度中:(待进一步进行选择)
  • 叶节点温度低:不打篮球(能直接确定为不打篮球)

2.2.2 子节点温度高的选择

    其剩下的数据集如下,温度不再进行下面的节点选择参与:

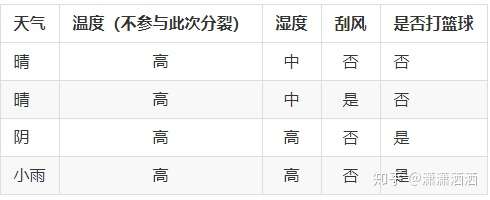
    根据信息熵的计算公式可以得到子节点温度高的信息熵为：

​ Ent(D)=-(2/4 * log2(2/4) + 2/4 * log2(2/4)) = 1.0

天气

    其数据表格如下:

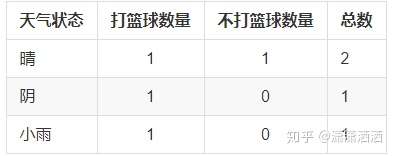
信息增益计算

    相应的信息熵如下：

D(晴天)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

D(阴天)=-(1/1 * log2(1/1) + 0/1 * log2(0/1)) = 0.0

D(雨天)=-(1/1 * log2(1/1) + 0/1 * log2(0/1)) = 0.0

    归一化信息熵为：

2/4 * 1.0 + 1/4 * 0.0 * 1/4 * 0.0 = 0.5

    其信息增益为：

Gain(天气)=1.0 - 0.5 = 0.5

信息增益率计算

    对应的属性熵为：

H(天气)=-(2/4 * log2(2/4) + 1/4 * log2(1/4) + 1/4 * log2(1/4)) = 1.5

    则其信息增益率为：

Gain_ratio(天气)=0.5/1.5=0.33333

基尼系数计算

• Gini(天气=晴)=1 - (1/2)^2 - (1/2)^2 = 1 - 1/4 - 1/4 = 0.5
• Gini(天气=阴)=1 - (1/1)^2 - (0/1)^2 = 0
• Gini(天气=小雨)=1 - (1/1)^2 - (0/1)^2 = 0
• Gini(天气)=2/4 * 0.5 + 1/4 * 0 + 1/4 * 0 = 0.25

湿度

    其数据表格如下:

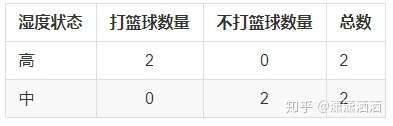
信息增益计算

    各情况的信息熵如下：

D(高)=-(2/2 * log2(2/2) + 0/2 * log2(0/2)) = 0.0

D(中)=-(0/2 * log2(0/2) + 2/2 * log2(2/2)) = 0.0

    作为子节点的归一化信息熵为：

2/4 * 0.0 + 2/4 * 0.0 = 0.0

    其信息增益为：

Gain(湿度)=1.0 - 0.0 = 1.0

信息增益率计算

    属性熵为：

H(湿度)=-(2/4 * log2(2/4) + 2/4 * log2(2/4) = 1.0

    则其信息增益率为：

Gain_ratio(湿度)=1.0/1.0=1.0

基尼系数计算

• Gini(湿度=高)=1 - (2/2)^2 - (0/2)^2 = 0
• Gini(湿度=中)=1 - (0/2)^2 - (2/2)^2 = 0
• Gini(湿度)=(2/4) * 0 + (2/4) * 0 = 0

刮风

    其数据表格如下:

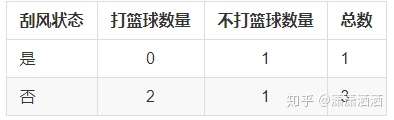
信息增益计算

    各情况的信息熵如下：

D(是)=-(0/1 * log2(0/1) + 1/1 * log2(1/1)) = 0

D(否)=-(2/3 * log2(2/3) + 1/3 * log2(1/3)) = 0.918

    作为子节点的归一化信息熵为：

1/4 * 0.0 + 3/4 * 0.918 = 0.688

    其信息增益为：

Gain(刮风)=1.0 - 0.688 = 0.312

信息增益率计算

    属性熵为：

H(刮风)=-(1/3 * log2(1/3) + 2/3 * log2(2/3) = 0.918

    则其信息增益率为：

Gain_ratio(刮风)=0.312/0.918=0.349

基尼系数计算

• Gini(刮风=是)=1 - (0/1)^2 - (1/1)^2 = 0

• Gini(刮风=否)=1 - (2/3)^2 - (1/3)^2 = 1 - 4/9 - 1/9 = 4/9

• Gini(刮风)=(1/4) * 0 + (3/4) * 4/9 = 1/3 = 0.333333

子节点温度高的选择

    如下汇总所有接口,第一个为信息增益的，第二个为信息增益率的，第三个为基尼系数的。其中信息增益和信息增益率选择最大的，基尼系数选择最小的。从下面的结果可以得到选择为：湿度

• Gain(天气)=1.0 - 0.5 = 0.5
• Gain(湿度)=1.0 - 0.0 = 1.0
• Gain(刮风)=1.0 - 0.688 = 0.312
• Gain_ratio(天气)=0.5/1.5=0.33333
• Gain_ratio(湿度)=1.0/1.0=1.0
• Gain_ratio(刮风)=0.312/0.918=0.349
• Gini(天气)=2/4 * 0.5 + 1/4 * 0 + 1/4 * 0 = 0.25
• Gini(湿度)=(2/4) * 0 + (2/4) * 0 = 0
• Gini(刮风)=(1/4) * 0 + (3/4) * 4/9 = 1/3 = 0.333333

    确定跟节点以后,大致的树结构如下，选择湿度作为分裂属性后能直接确定结果:

• 根节点
  • 子节点温度高
    • 叶节点湿度高：打篮球
    • 叶节点湿度中：不打篮球
  • 子节点温度中:(待进一步进行选择)
    • 叶节点温度低:不打篮球(能直接确定为不打篮球)

2.2.3 子节点温度中的选择

    其剩下的数据集如下,温度不再进行下面的节点选择参与:

    根据信息熵的计算公式可以得到子节点温度高的信息熵为：

Ent(D)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

天气

    其数据表格如下:

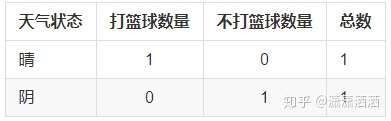
信息增益计算

    相应的信息熵如下：

D(晴天)=-(1/1 * log2(1/1) + 0/1 * log2(0/1)) = 0.0 D

(阴天)=-(0/1 * log2(0/1) + 1/1 * log2(1/1)) = 0.0

    归一化信息熵为：

1/2 * 0.0 + 1/2 * 0.0 = 0

    其信息增益为：

Gain(天气)=1.0 - 0 = 1.0

信息增益率计算

    对应的属性熵为：

H(天气)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

    则其信息增益率为：

Gain_ratio(天气)=1.0/1.0=1.0

基尼系数计算

• Gini(天气=晴)=1 - (1/1)^2 - (0/1)^2 = 0
• Gini(天气=阴)=1 - (0/1)^2 - (1/1)^2 = 0
• Gini(天气)=1/2 * 0.0 + 1/2 * 0.0 = 0

湿度

    其数据表格如下:

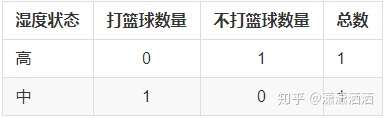
信息增益计算

    各情况的信息熵如下：

D(高)=-(0/1 * log2(0/1) + 1/1 * log2(1/1)) = 0.0

D(中)=-(1/1 * log2(1/1) + 0/1 * log2(0/1)) = 0.0

    作为子节点的归一化信息熵为：

1/2 * 0.0 + 1/2 * 0.0 = 0

    其信息增益为：

Gain(湿度)=1.0 - 0.0 = 1.0

信息增益率计算

    属性熵为：

H(湿度)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

    则其信息增益率为：

Gain_ratio(湿度)=1.0/1.0=1.0

基尼系数计算

• Gini(湿度=高)=1 - (0/1)^2 - (1/1)^2 = 0
• Gini(湿度=中)=1 - (1/1)^2 - (0/1)^2 = 0
• Gini(湿度)=1/2 * 0.0 + 1/2 * 0.0 = 0

刮风

    其数据表格如下:

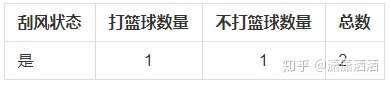
信息增益计算

    各情况的信息熵如下：

D(是)=-(1/2 * log2(1/2) + 1/2 * log2(1/2)) = 1.0

    作为子节点的归一化信息熵为：

1/1 * 1.0 = 1.0

    其信息增益为：

Gain(刮风)=1.0 - 1.0 = 0

信息增益率计算

    属性熵为：

H(刮风)=-(2/2 * log2(2/2) = 0.0

    则其信息增益率为：

Gain_ratio(刮风)=0/0 = 0

基尼系数计算

• Gini(刮风=是)=1 - (1/2)^2 - (1/2)^2 = 0.5
• Gini(刮风)=2/2 * 0.5 = 0.5

子节点温度中的选择

如下汇总所有接口,第一个为信息增益的，第二个为信息增益率的，第三个为基尼系数的。其中信息增益和信息增益率选择最大的，基尼系数选择最小的。从下面的结果可以得到天气和湿度是一样好的，我们随机选天气吧

• Gain(天气)=1.0 - 0 = 1.0
• Gain(湿度)=1.0 - 0.0 = 1.0
• Gain(刮风)=1.0 - 1.0 = 0
• Gain_ratio(天气)=1.0/1.0=1.0
• Gain_ratio(湿度)=1.0/1.0=1.0
• Gain_ratio(刮风)=0/0 = 0
• Gini(天气)=1/2 * 0.0 + 1/2 * 0.0 = 0
• Gini(湿度)=1/2 * 0.0 + 1/2 * 0.0 = 0
• Gini(刮风)=2/2 * 0.5 = 0.5

    确定跟节点以后,大致的树结构如下，选择天气作为分裂属性后能直接确定结果:

• 根节点
  • 子节点温度高
    • 叶节点湿度高：打篮球
    • 叶节点湿度中：不打篮球
  • 子节点温度中
    • 叶节点天气晴：打篮球
    • 叶节点天气阴：不打篮球
    • 叶节点温度低:不打篮球(能直接确定为不打篮球)

2.2.4 最终的决策树

    在上面的步骤已经进行完整的演示，得到当前数据一个完整的决策树：

• 根节点
  • 子节点温度高
    • 叶节点湿度高：打篮球
    • 叶节点湿度中：不打篮球
  • 子节点温度中
    • 叶节点天气晴：打篮球
    • 叶节点天气阴：不打篮球
    • 叶节点温度低:不打篮球(能直接确定为不打篮球)

3. 思考

 在构造的过程中我们可以发现，有可能同一个属性在同一级会被选中两次，比如上面的决策树中子节点温度高中都能选中温度作为分裂属性，这样是否合理？

 完整的构造整个决策树后，发现整个决策树的高度大于等于属性数量，感觉决策树应该是构造时间较长，但用于决策的时候很快，时间复杂度也就是O(n)