1.什么是特征选择
【特征选择】顾名思义就是对特征进行选择，以达到提高决策树学习的效率的目的。
【那么选择的是什么样的特征呢？】这里我们选择的特征需要是对训练数据有分类能力的特征，如果一个特征参与分类与否和随机分类的结果差别不大的话，我们就说这个特征没有分类能力，舍去这个特征对学习的精度不会有特别大的影响。
特征选择是决定用哪个特征来划分特征空间。
比如女生找男朋友，可能这个女生首先会问「这个男生帅不帅」，其次再是「身高如何」、「有无房子」、「收入区间」、「做什么工作」等等，那么「帅否」这个特征就是这位女生心中有着最好分类能力的特征了
【那怎么判断哪个特征有更好的分类能力呢？】这时候【信息增益】就要出场了。
2.信息增益
为了解释什么是信息增益，我们首先要讲解一下什么是【熵（entropy）】
熵（Entropy）
在热力学与化学中：
熵是一种测量在动力学方面【不能做功的能量的总数】，当总体熵增加，其做功能力也下降，熵的度量是能量退化的指标。
1948 年，香农把热力学中的熵引入到信息论中，称为香农熵。根据维基百科的描述：
在信息论中，熵是接收的每条消息中包含的信息的平均量。
更一般的，【熵表示随机变量的不确定性】。假设一个有限取值的离散随机变量 X 的概率分布如下：
那么它的熵定义为：
上式中的 b 通常取 2 或者自然对数 e，这时熵的单位就分别称为比特（bit）或纳特（nat），这也是信息论中，信息量的单位。
从上式中，我们可以看到，熵与 X 的取值是没有关系的，它只与 X 的分布有关，所以 H 也可以写作 p 的函数：
我们现在来看两个随机变量的情况。
假设随机变量 (X, Y) 的联合概率分布如下：
我们使用条件熵（conditional entropy）H(Y|X)来度量在已知随机变量 X 的条件下随机变量 Y 的不确定性。
条件熵定义为：X 给定条件下，Y 的条件概率分布的熵对 X 的数学期望。
是不是看晕了，没关系，我们来看数学公式，这才是最简单直接让你晕过去的方法：
有了上面的公式以后，条件熵的定义就非常容易理解了。
那么这些奇奇怪怪的熵又和我们要讲的信息增益有什么关系呢？
信息增益的定义与信息增益算法
既然熵是信息量的一种度量，那么信息增益就是熵的增加咯？
没错，由于熵表示不确定性，严格来说，信息增益（information gain）表示的是「得知了特征 X 的信息之后，类别 Y 的信息的不确定性减少的程度」。
我们给出信息增益的最终定义：
特征 A 对训练数据集 D 的信息增益 g(D, A)，定义为，集合 D 的经验熵 H(D) 与特征 A 给定条件下 D 的经验条件熵 H(D|A) 之差。
这里你只要知道经验熵和经验条件熵就是依据经验（由数据估计特别是极大似然估计）得出来的熵就可以了。
假设我们有一个训练集 D 和一个特征 A，那么，经验熵 H(D) 就是对 D 进行分类的不确定性，经验条件熵 H(D|A) 就是给定 A 后，对 D 分类的不确定性，经验熵 H(D) 与经验条件熵 H(D|A) 的差就是信息增益。
很明显的，不同的特征有不同的信息增益，信息增益大的特征分类能力更强。我们就是要根据信息增益来选择特征。
ps：信息增益体现了特征的重要性，信息增益越大说明特征越重要
信息熵体现了信息的不确定程度，熵越大表示特征越不稳定，对于此次的分类，越大表示类别之间的数据差别越大
条件熵体现了根据该特征分类后的不确定程度，越小说明分类后越稳定
信息增益=信息熵-条件熵，越大说明熵的变化越大，熵的变化越大越有利于分类
下面我们给出信息增益的算法。
首先对数据做一些介绍：
- 假设我们有一个训练集 D，训练集的总的样本个数即样本容量为 |D|，最后的结果有 K 个类别，每个类别表示为
，
为属于这个类的样本的个数，很显然
。
- 再假设我们有一个特征叫 A，A 有 n 个不同的取值
，那么根据 A 我们可以将 D 分成 n 个子集，每个子集表示为
，
是这个子集的样本个数，很显然
。
- 我们把
，
是其样本个数。
信息增益的计算就分为如下几个步骤：
- 计算 D 的经验熵 H(D)：
\2. 计算 A 对 D 的经验条件熵 H(D|A)：
\3. 计算信息增益 g(D, A)：
3.信息增益比
看到这个小标题，可能有人会问，信息增益我知道了，信息增益比又是个什么玩意儿？
按照经验来看，【以信息增益准则来选择划分数据集的特征，其实倾向于选择有更多取值的特征，而有时这种倾向会在决策树的构造时带来一定的误差】。
ps：信息增益体现了特征的重要性，信息增益越大说明特征越重要。类别越多代表特征越不确定，即熵越多，类别的信息增益越小。
为了校正这一误差，我们引入了【信息增益比（information gain ratio）】，又叫做信息增益率，它的定义如下：
特征 A 对训练数据集 D 的信息增益比 定义为其信息增益
与训练数据集 D 关于特征 A 的值的熵
之比。
其中， ，n 是 A 取值的个数。
两个经典的决策树算法 ID3 算法和 C4.5 算法，分别会采用信息增益和信息增益比作为特征选择的依据。
4. ID3 ： 最大信息增益
ID3以信息增益为准则来选择最优划分属性
信息增益的计算要基于信息熵（度量样本集合纯度的指标）
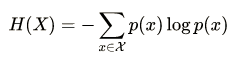信息熵越小，数据集X的纯度越大
因此，假设于数据集D上建立决策树，数据有K个类别：
公式（1）中：
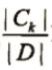表示第k类样本的数据占数据集D样本总数的比例
公式（2）表示的是以特征A作为分割的属性，得到的信息熵：
Di表示的是以属性A为划分，分成n个分支，第i个分支的节点集合
因此，该公式求的是以属性A为划分，n个分支的信息熵总和
公式（3）为分割后与分割前的信息熵的差值，也就是信息增益，越大越好
但是这种分割算法存在一定的缺陷：
假设每个记录有一个属性“ID”，若按照ID来进行分割的话，由于ID是唯一的，因此在这一个属性上，能够取得的特征值等于样本的数目，也就是说ID的特征值很多。那么无论以哪个ID为划分，叶子结点的值只会有一个，纯度很大，得到的信息增益会很大，但这样划分出来的决策树是没意义的。由此可见，ID3决策树偏向于取值较多的属性进行分割，存在一定的偏好。为减小这一影响，有学者提出C4.5的分类算法。
5. C4.5 ：最大信息增益率
C4.5基于信息增益率准则选择最优分割属性的算法
信息增益比率通过引入一个被称作【分裂信息(Split information)】的项来惩罚取值较多的属性。
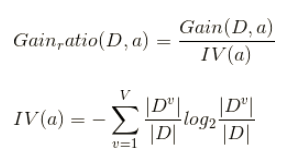
上式，分子计算与ID3一样，分母是由属性A的特征值个数决定的，个数越多，IV值越大，信息增益率越小，这样就可以避免模型偏好特征值多的属性，但是聪明的人一看就会发现，如果简单的按照这个规则来分割，模型又会偏向特征数少的特征。因此C4.5决策树先从候选划分属性中找出信息增益高于平均水平的属性，在从中选择增益率最高的。
对于连续值属性来说，可取值数目不再有限，因此可以采用离散化技术（如二分法）进行处理。将属性值从小到大排序，然后选择中间值作为分割点，数值比它小的点被划分到左子树，数值不小于它的点被分到又子树，计算分割的信息增益率，选择信息增益率最大的属性值进行分割。
6.CART ：最小基尼指数
CART以基尼系数为准则选择最优划分属性，可以应用于分类和回归
CART是一棵二叉树，采用【二元切分法】，每次把数据切成两份，分别进入左子树、右子树。而且每个非叶子节点都有两个孩子，所以CART的叶子节点比非叶子多1。相比ID3和C4.5，CART应用要多一些，既可以用于分类也可以用于回归。CART分类时，使用基尼指数（Gini）来选择最好的数据分割的特征，gini描述的是纯度，与信息熵的含义相似。CART中每一次迭代都会降低GINI系数。
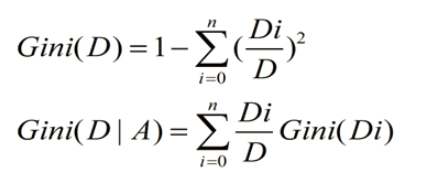Di表示以A是属性值划分成n个分支里的数目
Gini(D)反映了数据集D的纯度，值越小，纯度越高。我们在候选集合中选择使得划分后基尼指数最小的属性作为最优化分属性。
7.分类树和回归树
提到决策树算法，很多想到的就是上面提到的ID3、C4.5、CART分类决策树。其实决策树分为分类树和回归树，前者用于分类，如晴天/阴天/雨天、用户性别、邮件是否是垃圾邮件，后者用于预测实数值，如明天的温度、用户的年龄等。
作为对比，先说分类树，我们知道ID3、C4.5分类树在每次分枝时，是穷举每一个特征属性的每一个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值。按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。
回归树总体流程也是类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差–即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。
